Second Preimage Attack against Merkle Trees

I recently spent some time learning about the practical implementation details of Merkle trees. One thing that I found underdocumented and required some thinking was the concept of “second preimage attacks” against Merkle trees. This is an attack which requires changes to the naive design for implementing this tree. I am documenting it here in hopes that it will be more clear to others implementing it.

A Merkle tree is a type of tree in which every leaf node is the hash of a block of input data. Every branch node is the hash of the concatenation of its child values.

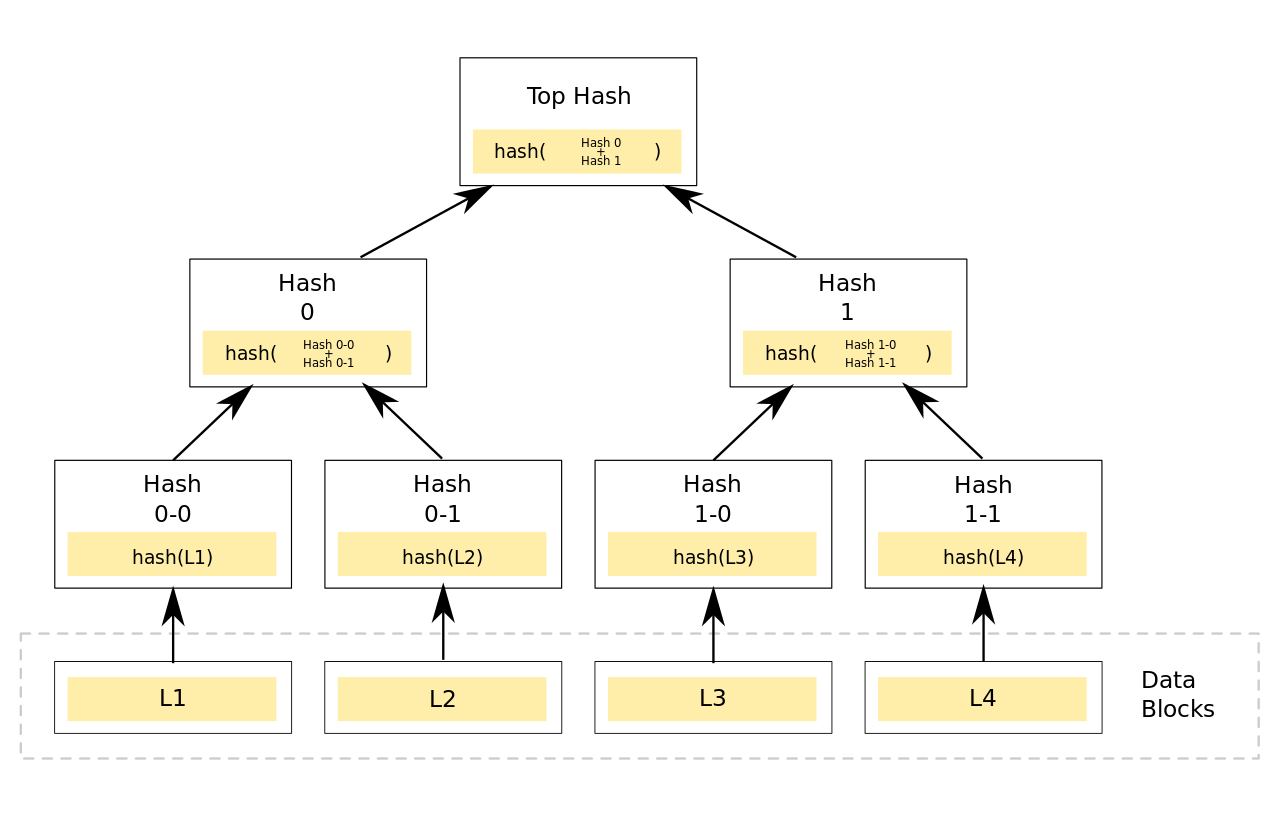
Picture of a Merkle Tree. Taken from https://en.wikipedia.org/wiki/File:Hash_Tree.svg and licensed under CC0. This example is vulnerable to a second preimage attack.

Merkle trees are useful because they allow for the efficient verification of large amounts of data. To verify, from the picture above, that L1, L2, L3, and L4 were all received successfully, the Top Hash is all that is needed. This is bog-standard hashing and not impressive. Where this becomes valuable is if you start with the Top Hash and want to validate the contents of L1 through L4. Making it more complex, each of the data blocks can be received independently of one another. This is a common situation in file sharing protocols such as Bitorrent and DC++.

To check each of the data blocks a validator needs to know their corresponding leaf node from the tree. L1 corresponds to Hash 0-0 such that if you know the value of Hash 0-0 the validator knows they received L1 successfully. However all that the validator is starting with is the Top Hash. With the Top Hash however you can work your way down the tree. Assuming the hash algorithm is a cryptographic hash, and collisions are infeasible, it is possible to validate Hash 0 and Hash 1 by checking that the hash of their concatenation matches the Top Hash. By repeating this it is possible to work ones way down the tree, even in environments where the validator may not trust the other party telling it the branch and leaf hash values. Other clever optimizations exist, a reader can check Wikipedia or read a textbook for more information.

Second Preimage Attack

All this brings us to the second preimage attack. A second preimage attack is as follows: Given a hash function H() and two inputs x and x' where x != x', H(x) = H(x'). Hash functions such as SHA-256 have second preimage resistance, the discovery of x and x' being difficult, as a core property.

If a Merkle tree is implemented naively, with a single function such as SHA-256 being used for every node, it is vulnerable to a second preimage attack. That is the implementation as shown in the picture above. Assume for the purposes of this attack the attacker knows every value in the Merkle tree: top hash, hash 0, hash 1, hash 0-0, etc. An adversary can now create a new data block E1 = Hash 0-0 + Hash 0-1.

An illustration of the attack. “||” is used to represent concatenation and Hash_F represents the hash function.

When a victim comes looking for the tree values that correspond to top hash the adversary can provide Hash 0, Hash 1, Hash 1-0 and Hash 1-1. These values will all be validated as being under top hash. The trap is now sprung. Instead of providing Hash 0-0 and Hash 0-1 the adversary claims that Hash 0 is a leaf node. There is no information about the depth of a tree or leaf vs. branch nodes stored in a naive Merkle tree implementation. The attacker then provides E1, L3, and L4 as the data blocks. L1 and L2 have been lost and a second preimage attack has occurred. It is possible to also carry this out to not provide L3 and L4 as well, allowing for an attacker to carry out a complete second preimage attack with no knowledge of the L data blocks.

Defenses

There are several possible defenses against a second preimage attack. Some of these are as follows:

• Mix information about the node type into the hash: This is what is done for Certificate Transparency (https://datatracker.ietf.org/doc/html/rfc9162) where 0x00 is prepended to leaf nodes. 0x01 is prepended to branch nodes.
  • I like this approach because it is straightforward to implement. See below for a description of why it works.
• Require a defined depth: Agree upon a depth that the tree must have. A data block is valid if and only if the nodes leading to the leaf, which has the hash of the data block, are of the defined depth.
  • This works for trees that can be of a uniform depth, i.e. chunks of a large file. This does not work as well for other situations, for example if the Merkle tree is over a filesystem and branch nodes represent folders that can be arbitrarily nested.

Why does prepending information work?

Under Defenses I stated that prepending information on if a node is a leaf or branch fixes the second preimage attack vulnerability. This section explores why that is the case.

For this section I will define two new hash functions, based on the prior hash functions.

• Hash_L for the Leaf nodes. This is defined as Hash_L = Hash('A' || Input)
• Hash_B for the Branch nodes. This is defined as Hash_B = Hash('B' || Input)

A simple tree now looks like the following:

Binary Merkle tree with 4 data elements. Each hash is either Hash_L for leaf nodes or Hash_B for branch nodes.

To make this example more real, I will assign values to each of the nodes and calculate the hashes based on that. I will use SHA-256 as the hash function of choice.

• L1 = “Foo”
• L2 = “Bar”
• L3 = “Baz”
• L4 = “Qux”
• Hash 0-0 = Hash_L(L1) = SHA-256("AFoo") = c394c83b94a489485a0ea7dbfd43d6b18a7cd6ef7a4d607f5c667e978a232d07
• Hash 0-1 = Hash_L(L2) = SHA-256("ABar") = 2fa32a6f44e6ed4e6357e25c7fae397d51028cbb1ea527f1831439eaeefdb64a
• Hash 1-0 = Hash_L(L3) = SHA-256("ABaz") = bf2d89291058bc1e2e5cd3255dcc3d0d39eb1a54623c268e9adf892b903f38e7
• Hash 1-1 = Hash_L(L4) = SHA-256("AQux") = eb5e40d6a93d1db9ab45db84465bd5809064741588415d46c817b3bdd338ce1f
• Hash 0 = Hash_B( Hash 0-0 || Hash 0-1 ) = SHA-256("Bc394c83b94a489485a0ea7dbfd43d6b18a7cd6ef7a4d607f5c667e978a232d072fa32a6f44e6ed4e6357e25c7fae397d51028cbb1ea527f1831439eaeefdb64a") = ca10d813fdb6e755f9a0984b53a7600c49b2fc6aaba028ddc90b8d4a7b766242
• Hash 1 = Hash_B( Hash 1-0 || Hash 1-1 ) = SHA-256("Bbf2d89291058bc1e2e5cd3255dcc3d0d39eb1a54623c268e9adf892b903f38e7eb5e40d6a93d1db9ab45db84465bd5809064741588415d46c817b3bdd338ce1f") = a9d8f95ea21aff1147359ca4a040f39aa21fc951e942466b0861bf14486db4f5
• Top Hash = Hash_B( Hash 0 || Hash 1 ) = SHA-256("Bca10d813fdb6e755f9a0984b53a7600c49b2fc6aaba028ddc90b8d4a7b766242a9d8f95ea21aff1147359ca4a040f39aa21fc951e942466b0861bf14486db4f5") = c21243ead9185756bac406d7c6132479c27a0f3bfbd378ffbd28b3596ba7a313

So now the Top Hash is known to be c21243ead<etc>. What happens when an attacker creates E1?

Attempting the second preimage attack with the Hash_B and Hash_L functions.

The important part to note here is that Hash 0 no longer has child nodes. That means that it’s hash function has changed from Hash_B to Hash_L. This in turn means that the new value of Hash 0 is SHA-256("Ac394c83b94a489485a0ea7dbfd43d6b18a7cd6ef7a4d607f5c667e978a232d072fa32a6f44e6ed4e6357e25c7fae397d51028cbb1ea527f1831439eaeefdb64a") = 1d0048fc197f5848147a93f19ef7ce1107e2df37ca0d2b6c5cc2c2ada004d5aa. This is different from the original Hash 0 and will fail a verification when combined with the Hash 1 value to check against Top Hash. This simple change has removed the attack vector.

References

• https://en.wikipedia.org/wiki/Merkle_tree#Second_preimage_attack
• https://crypto.stackexchange.com/questions/2106/what-is-the-purpose-of-using-different-hash-functions-for-the-leaves-and-interna
  • I found it confusing that the author of the question described this as “two different hash functions be used”. I think a better wording would be “why would I prepend different data for the node type”.